ニュートン法による複素求根アルゴリズム~Pythonコード付き~

ニュートン法 (求根アルゴリズム)
方程式の解を求める方法(求根アルゴリズム)の最も有名なものに、ニュートン法(Newton’s method)またはニュートン・ラフソン法(Newton-Raphson method)があります。これは
$$f(x) = 0$$
となる方程式の解\(x\)を求める手法で、具体的には\( x_0 \)を解の十分近くの値として適当に設定し、
$$ x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)} \tag{1}$$
のように、\( x_0, x_1, x_2\cdots \)を逐次的に求めていき、解の近似値を得ます。
なぜ式(1)のような形になるかは、次のように\(f(x) = 0 \)を\(x = x_0 \)の周りで1次の項までテイラー展開することで分かります。
$$ f(x) \approx f(x_0) + (x – x_0) f'(x_0) = 0$$
$$ x = x_0 – \frac{f(x_0)}{f'(x_0)} $$
上式で、得られた値\(x\)(=左辺)を再び右辺に代入して、繰り返し計算していきます。
解きたい方程式の解の範囲を複素数まで拡張した場合も、ニュートン法を適用することで複素数解を求めることができます。ただしその場合、初期値の近傍の解に収束するとは限りません。複素平面上での各点を初期値とし、解きたい方程式の解を複素平面にプロットすると、『ニュートンフラクタル』という奇妙な図形が現れます。以下に、Pythonでのニュートン法のコードと、ニュートンフラクタルの一例を示します。
ニュートン法の計算プログラム(Python)
以下のプログラムでは、
$$f(z) = z^5 +1 $$
を例に、初期値\(z_0\)を\(\{ z \mid -1<Re(z)<1, -1<Im(z)<1 \} \)の範囲でニュートン法を適用し、根の偏角の大きさをカラーマップで表示しています。
# -*- coding: utf-8 -*-
"""
複素平面上の値を初期値として、方程式func(z)=0の根zをニュートン法で計算し、
その偏角の大きさを2次元カラーマップする。
"""
import numpy as np
import matplotlib.pyplot as plt
# 初期値z0の計算範囲
real_min = -1 # 実部最小値
real_max = 1 # 実部最大値
im_min = -1 # 虚部最小値
im_max = 1 # 虚部最大値
# 計算範囲の分割数
N_real = 1000 # 実部方向
N_im = 1000 # 虚部方向
def newton_method(z):
f = z**5 + 1 # 根を求めたい関数
df = 5 * z**4 # 関数の1階導関数
if df!=0:
return z - f/df # z1 = z0 - f(z0)/f'(z0)
else:
return 0 # 導関数が0のときはニュートン法を適用できない
# 収束するまでnewthon_method()を繰り返す
def root_of_func(z):
counter = 0
while True:
z_new = newton_method(z)
eps = abs(z_new - z)
if eps < abs(real_max - real_min)*1E-10: # 収束条件
break
if counter == 100: # 計算回数の上限
break
z = z_new
counter += 1
return z_new
# 複素平面上で、偏角の大きさを2次元カラーマップする
def plot_complex(complex_func):
x, y = np.meshgrid(np.linspace(real_min,real_max, N_real), np.linspace(im_min,im_max, N_im))
z = x + y*1j
solutions = np.zeros_like(z)
for ix in range(N_real):
for iy in range(N_im):
solutions[iy][ix] = root_of_func(z[iy][ix]) # 各初期値に対して、ニュートン法を実施
print("ix=",ix,"/",N_real) # 進捗率表示
angles = (np.angle(solutions) + 2*np.pi) % (2*np.pi)*180/np.pi # 0~360度の範囲で表記
plt.figure(figsize=(4, 4), dpi=600)
im = plt.imshow(angles, origin="lower", cmap="hsv",
vmin=0,vmax=360,extent=[real_min,real_max,im_min,im_max])
plt.xlabel("Real part")
plt.ylabel("Imaginary part")
cbar=plt.colorbar(im, fraction=0.046, pad=0.04) # colorbarのサイズと位置調整
cbar.set_label('Argument (°)',size=10)
plot_complex(root_of_func)
以下に計算結果を示します。
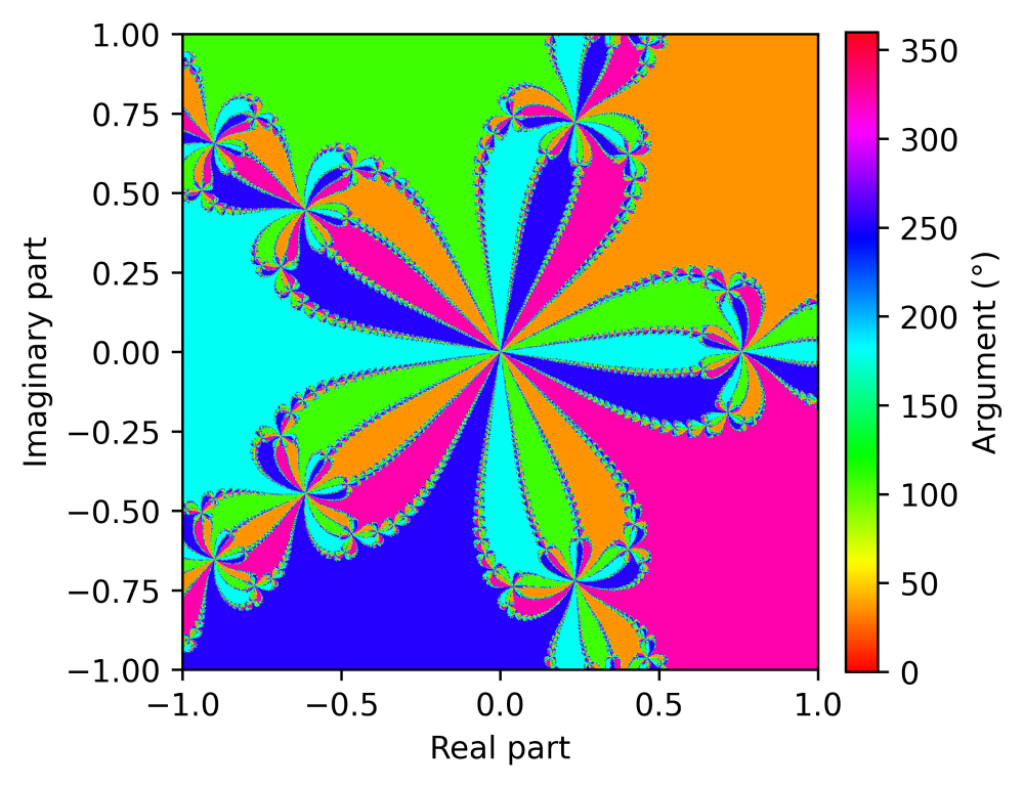
複素数の範囲でニュートン法を適用すると、上図のようにニュートンフラクタルという複雑な図形が現れます。その他の方程式でも様々な図形が現れて非常に面白いので、上記のPythonプログラムをコピペして、いろいろ試してみてください。
関連記事
-
前の記事

時間を効率的に使う方法【TED-Ed】英語で学ぶ 2021.03.05
-
次の記事

コロナ禍でのオンライン学会 2021.03.13
