Jenkins-Traubアルゴリズムで多項式の根を求める~Pythonコード付き~

多項式の根を求めるアルゴリズムの一つ、Jenkins-Traub法(ジェンキンズ-トラウブ法)の導出方法と、Pythonでの実行コードについて解説する。
Jenkins-Traubアルゴリズムの導出
求根アルゴリズムの一つであるJenkins-Traub法とは、\(n\)次の多項式\(p(z)\)の根、すなわち\(p(z)=0\)の解\(z\)を求める手法のひとつである。
$$ p(z) = z^n + a_1 z^{n-1} + \cdots + a_{n-1}z + a_n $$
\(p(z)\)の根を\(\alpha_j\)、重根度を\(m_j\)とすると、\(p(z)\)は以下のように表せる。
$$p(z) =\prod_{j=1}^k (z – \alpha_j)^{m_j}$$
\(p(z)\)を\(z\)で微分する。
$$ \begin{eqnarray}
p'(z) &=& \sum_{j=1}^k m_j \frac{p(z)}{z-\alpha_j} \\
&=& \sum_{j=1}^k m_j P_j(z) \\
\Bigl( P_j(z) &=& \frac{p(z)}{z-\alpha_j} \Bigr) \tag{1} \\
\end{eqnarray} $$
ここで次のような多項式列\( \{H^{(\lambda)}(z) \}_{\lambda} \)を考える。
$$ \begin{eqnarray}
H^{(0)}(z) &=& p'(z) \\
H^{(\lambda)}(z) &=& \sum_{j=1}^k c_j^{(\lambda)} P_j (z) \tag{2} \\
\end{eqnarray} $$
係数\(c_j^{(\lambda)} \)については、下記を満たすようなものをとる。
$$ \begin{eqnarray}
c_j^{(0)} &=& m_j \ \ (j=1,2,\cdots ,k) \\
\Bigl( d_j^{(\lambda)} &=& \Bigr) \frac{c_j^{(\lambda)}}{c_1^{(\lambda)}} \xrightarrow[\lambda \xrightarrow{} \infty]{} 0 \ \ (j=2,\cdots ,k) \tag{3}\\
\end{eqnarray} $$
すると\(H^{(\lambda)}(z)\)は、
$$ H^{(\lambda)}(z) \xrightarrow[\lambda \xrightarrow{} \infty]{} c_1^{(\lambda)}P_1(z) \tag{4} $$
となる。
このとき、次式で定義される数列\( \{ t_{\lambda} \}_{\lambda} \)は根\(\alpha_1\)に近づく。(*)
$$ \begin{eqnarray}
t_{\lambda +1} &=& s_{\lambda} \ – \ \frac{p(s_\lambda)}{\widetilde{H}^{(\lambda +1)}(s_{\lambda})} \tag{5} \\
\widetilde{H}^{(\lambda)}(z) &=& \frac{H^{(\lambda)}(z)}{\sum_{j=1}^k c_j^{(\lambda)}} \tag{6}
\end{eqnarray} $$
式(5)の\( \{ s_{\lambda} \}_{\lambda}\)は任意の複素数列である。
(*)の証明
式(5)に式(6)を代入すると、
$$ t_{\lambda +1} = s_{\lambda} \ – \ \frac{ \sum_{j=1}^k c_j^{(\lambda +1)} p(s_\lambda)}{H^{(\lambda +1)}(s_{\lambda})} $$
となる。さらに、式(1)で\(j=1\)とした\( \ p(s_{\lambda})=(s_{\lambda} – \alpha_1)P_1(s_{\lambda}) \ \)と式(2)を代入すると、
$$ \begin{eqnarray}
t_{\lambda +1} &=& s_{\lambda} \ – \ \frac{ \sum_{j=1}^k c_j^{(\lambda +1)} (s_{\lambda} – \alpha_1)P_1(s_{\lambda}) }{ \sum_{j=1}^k c_j^{(\lambda +1)} P_j(s_{\lambda})} \\
&=& s_{\lambda}\ – \ \frac{ (s_{\lambda}-\alpha_1) P_1(s_{\lambda}) c_1^{(\lambda+1)} (1+\sum_{j=2}^k d_j^{(\lambda +1)} ) }{ c_1^{(\lambda +1)} P_1(s_{\lambda}) ( 1+ \sum_{j=2}^k d_j^{(\lambda +1)} \frac{P_j(s_{\lambda})}{P_1(s_{\lambda})} ) } \\
& \xrightarrow[\lambda \xrightarrow{} \infty]{} & s_{\lambda} \ – \ (s_{\lambda} – \alpha_1) = \alpha_1
\end{eqnarray} $$
((*)の証明終了)
次に\( \widetilde{H}^{(\lambda)} (z)\)および\(H^{(\lambda)}(z) \)の具体的な形について考えてみる。
式(1)より\( P_j(z) \)の最大次数は\( (n-1) \)であり、その\( (n-1) \)次の項の係数は\( 1\)である。そして、式(2)より\(H^{(\lambda)}(z)\)も\( (n-1) \)次の多項式である。\( \widetilde{H}^{(\lambda)} (z)\)については式(6)より\(H^{(\lambda)}(z)\)と同様に\( (n-1) \)次の多項式であり、さらに式(6)に式(3),(4)を適用することで、
$$ \widetilde{H}^{(\lambda)} (z) \xrightarrow[\lambda \xrightarrow{} \infty]{} P_1(z) $$
となるので、\(\lambda\)が十分大きいときには\( \widetilde{H}^{(\lambda)} (z)\)の\( (n-1) \)次の項の係数は\( P_1(z) \)と同様に\(1\)となる。すなわち\( \widetilde{H}^{(\lambda)} (z)\)は、\(H^{(\lambda)}(z)\)を\( (n-1) \)次の項の係数が\(1\)になるように規格化することで求められる。
そして、式(4)を満たすような多項式列\( \{H^{(\lambda)}(z) \}_{\lambda} \)については次のような漸化式を用いてやればよい。
$$ H^{(\lambda+1)}(z) = \frac{1}{z-s_{\lambda}} \Bigl[ H^{(\lambda)}(z) – \frac{H^{(\lambda)}(s_{\lambda})}{p(s_{\lambda})}p(z) \Bigr] \tag{7} $$
[・・・]内は\(z=s_{\lambda}\)の時\(0\)になるため\( (z-s_{\lambda}) \)で割り切れる。すなわち、すべての\( \lambda\)について式(7)で定義される多項式列\( \{H^{(\lambda)}(z) \}_{\lambda} \)は\( (n-1) \)次の多項式である。
式(7)より
$$ \begin{eqnarray}
H^{(\lambda+1)}(z) &=& \frac{p(z)}{z-s_{\lambda}} \Bigl[ \ \sum_{j=1}^{k} \frac{c_j^{(\lambda)}}{z-\alpha_j} \ – \ \sum_{j=1}^{k} \frac{c_j^{(\lambda)} }{s_{\lambda}-\alpha_j} \ \Bigr] \\
&=& \frac{p(z)}{z-s_{\lambda}} \sum_{j=1}^{k} \frac{ c_j^{(\lambda)} (s_{\lambda}-z) }{(z-\alpha_j)(s_{\lambda}-\alpha_j) } \\
&=& p(z)\sum_{j=1}^{k} \frac{ c_j^{(\lambda)} }{(z-\alpha_j)(\alpha_j-s_{\lambda} )} \\
&=& \sum_{j=1}^{k} P_j(z)\frac{ c_j^{(\lambda)} }{(\alpha_j-s_{\lambda} ) } \\
\end{eqnarray} $$
式(2)で\(\lambda \xrightarrow{} \lambda+1 \) としたものと上式を比較すると、
$$ \begin{eqnarray}
c_j^{(\lambda+1)} &=& \frac{ c_j^{(\lambda)} }{ \alpha_j \ – \ s_{\lambda} } \\
&=& \frac{ c_j^{(\lambda-1)} }{ (\alpha_j \ – \ s_{\lambda})(\alpha_j \ – \ s_{\lambda-1}) } \\
& \cdots& \\
&=& \frac{c_j^{(0)}}{\prod_{l=0}^{\lambda} (\alpha_j \ – \ s_l)} \\
&=& \frac{m_j}{\prod_{l=0}^{\lambda} (\alpha_j \ – \ s_l )}
\end{eqnarray} $$
\(\{s_{\lambda}\}\)は任意の複素数列なので、根\(\alpha_1\)に収束する数列\(\{t_{\lambda}\}\)とすれば
$$ \begin{eqnarray}
|c_1^{(\lambda)}| &\xrightarrow{}& \infty \ \ (\lambda \xrightarrow{} \infty)\\
|c_j^{(\lambda)}| &<& \infty \ \ (j=2,3,\cdots,k) \\
\end{eqnarray} $$
となり、式(3)および式(4)が満たされていることがわかる。
参考文献:
Mekwi, Wankere R. “Iterative methods for roots of polynomials.” (2001).
Jenkins–Traub algorithm – Wikipedia
関連記事:
ニュートン法による複素求根アルゴリズム~Pythonコード付き~
Jenkins-Traub法のPythonコード
以下のプログラムでは、
$$p(z) = z^5 +1 $$
を例に、初期値\(z_0\)を\(\{ z \mid -10<Re(z)<10, -10<Im(z)<10 \} \)の範囲でJenkins-Traub法を適用し、根の偏角の大きさをカラーマップで表示しています。
# -*- coding: utf-8 -*-
"""
『Jenkins Traub法』で複素平面の各点を初期値としてp(z)の根を求め、その偏角をカラーマップにする
"""
import numpy as np
import matplotlib.pyplot as plt
LIMIT = 100 # 計算回数の上限
EPS = 1E-10 # ゼロ点の判定範囲. abs(p(z)) < eps ならばゼロ点とする.
p = np.poly1d([1,0,0,0,0,1]) # p(z) = z^5 + 1
dp = p.deriv() # 微分
print(p)
# 初期値の計算範囲
real_min=-10
real_max=-real_min
im_min=-10
im_max=-im_min
# ステップ数
N_real=500
N_im=500
# 複素平面の各点を初期値として、p(z)の根を求めその偏角をカラーマップにする
def plot_complex(complex_func):
x, y = np.meshgrid(np.linspace(real_min,real_max, N_real), np.linspace(im_min,im_max, N_im))
z = x + y*1j
solutions = np.zeros_like(z)
for ix in range(N_real):
for iy in range(N_im):
solutions[iy][ix] = Root_of_func(z[iy][ix])
print(ix,"/",N_real-1)
angles = (np.angle(solutions) + 2*np.pi) % (2*np.pi) *180/np.pi
plt.figure(figsize=(4, 4), dpi=300)
im = plt.imshow(angles, origin="lower",cmap="hsv",vmin=0,vmax=360,\
extent=[real_min,real_max,im_min,im_max])
plt.colorbar(im, fraction=0.046, pad=0.04)
return angles
# Jenkins Traub法
def Root_of_func(z):
H = dp # 多項式H0(z)
s = z # s0
counter = 0
while True:
numerator = H - p*H(s)/p(s) # H(s):Hλ(s), s:s_λ
denominator = np.poly1d([1,-s]) # z-s
H_new, remainder = np.polydiv(numerator,denominator) # 多項式の除算
H_new /= H_new.c[0]
s += -p(s)/H_new(s)
if abs(p(s)) <EPS or counter==LIMIT:
break
H = H_new
counter += 1
return s
ang = plot_complex(Root_of_func)
以下に計算結果を示します。
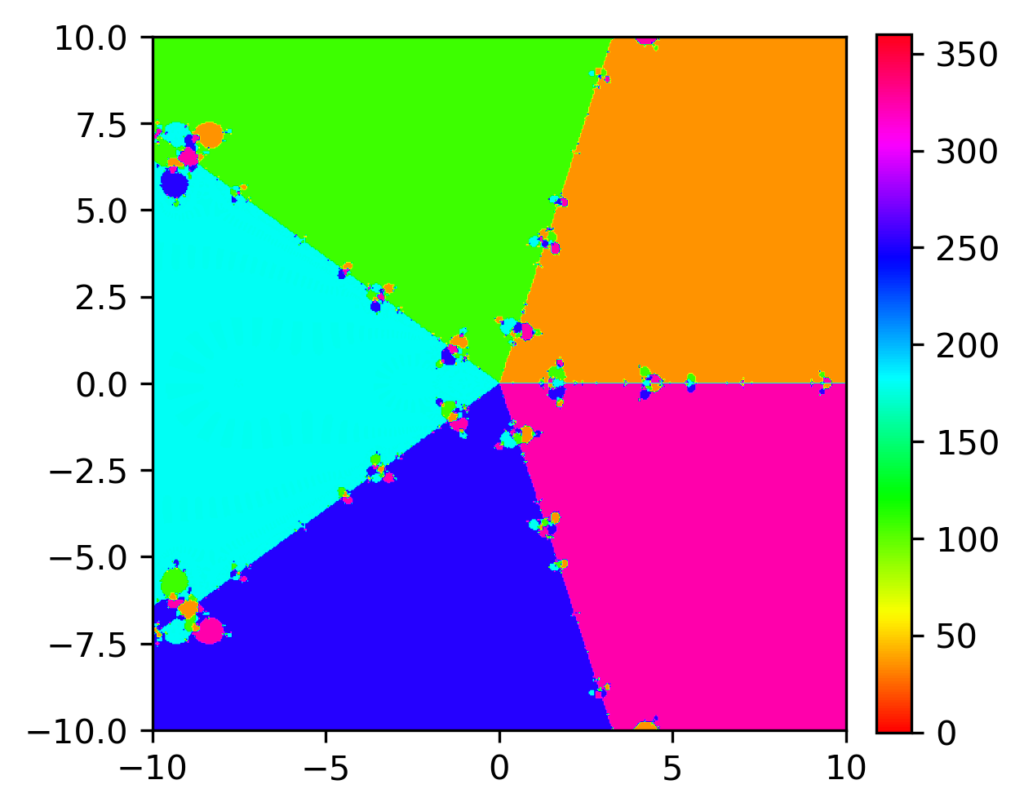
他の方程式にすると全く変わった図形が現れて非常に面白いので、上記のPythonプログラムをコピペして、いろいろ試してみてください。
-
前の記事
ラゲール法による求根アルゴリズム~Pythonコード付き~ 2021.03.17
-
次の記事

ニュートン法で関数のすべての複素根を求める-Pythonプログラム 2021.03.21
